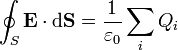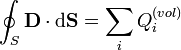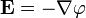Elektrostatika
Elektrostatika je část fyziky, která studuje elektrické jevy, které souvisejí s (časově) ustáleným (neměnným) vzájemným silovým působením elektricky nabitých částic a těles. V širším slova smyslu se do elektrostatiky řadí i jevy elektrizace těles a (i nestatické) projevy tzv. statické elektřiny.
Základním pojmem elektrostatiky je statické elektrické pole, které lze popsat pomocí vektorového pole intenzity elektrického pole nebo pomocí skalárního potenciálu.
Základním zákonem elektrostatiky je Coulombův zákon, ze kterého lze odvodit další zákony a věty elektrostatiky.
Jevy souvisejícími s proměnným elektrickým polem (jakož i elektromagneticky indukovaným statickým elektrickým polem) se zabývá elektrodynamika.
Elektrostatické jevy
Přitahování a odpuzování nabitých těles

Již od starověku, přesněji od 6. století př. n. l., kdy řecký filozof Thales pozoroval přitažlivé síly, vznikající jako následek tření jantaru [1], jsou popsány projevy přitažlivých a odpudivých sil mezi zelektrovanými tělesy. Řecké slovo pro jantar je ήλεκτρον (elektron), toto slovo se posléze stalo zdrojem pro novější slovo "elektřina". V současném pojetí označujeme jako zdroje těchto sil elektrické náboje, které třením na površích některých materiálů vznikají. Platí přitom, že existují dva druhy elektrického náboje (kladný a záporný), přičemž dva náboje stejného druhu se odpuzují, dva náboje opačného druhu naopak přitahují. Dva druhy „elektřiny“ poprvé rozlišil Charles Francois Dufay.
První měření elektrického silového působení prováděl William Gilbert, který ho první odlišil od působení magnetického a který také zavedl pojem elektřina. Zákonitosti silového působení nezávisle na sobě kvantitativně popsali Henry Cavendish a Charles August Coulomb, podle kterého je nazván Coulombův zákon .
Třebaže elektrostatické síly se zdají býti dosti slabé, elektrostatická síla působící mezi elektronem a protonem v jádře vodíkového atomu je asi o 40 řádů silnější než jejich vzájemné gravitační přitahování.
Elektrostatické silové působení je možné demonstrovat na příkladech, jako je přilnavost silonového sáčku k ruce, při česání suchých vlasů hřebenem přitažlivost vlasů a hřebenu nebo hromadění polétavého prachu na televizní obrazovce. Na principu elektrického odpuzování souhlasných nábojů je založen elektroskop. Elektrostatické přitažlivé síly jsou využívány v xerografii (v kancelářských kopírkách a tiskárnách) nebo v elektrostatických odlučovačích (filtrech) např. u průmyslových kouřovodů.
Následující jevy jsou založeny na skutečnosti, že hmotná látka je na mikroskopické úrovni tvořena z nabitých částic.
Elektrostatická indukce
Vložením vodiče (tj. látky, ve které se elektrický náboj, přesněji nabitá částice, může volně přesouvat) do elektrického pole jiného nabitého tělesa se toto pole změní. Příčinou je přeskupení volných nabitých částic ve vodiči, nazývané elektrostatická indukce. Bez vlivu vnějšího pole jsou v nenabitém vodiči nosiče kladného i záporného náboje rovnoměrně rozloženy. Vlivem odpudivých sil se nosiče náboje souhlasného s nábojem nabitého tělesa přesunou na protilehlou část vodiče, naopak nosiče náboje opačného se přitáhnou do přilehlé části vodiče. Vznik dvou seskupení opačných nábojů indukcí lze prokázat oddělením přilehlé a protilehlé části vodiče a po odstranění vnějšího pole změřením indukovaného náboje na každé části elektroskopem.
Ze stejného důvodu se v elektricky nabitém vodiči všechny nosiče „přebývajícího“ náboje rozprostřou vzájemným odpuzováním na jeho povrchu, tj. co nejdále od sebe.
Na principu elektrostatické indukce pracuje Indukční elektrika Wimshurstova a je něm též založen kondenzátor, poprvé zkonstruovaný E. Kleistem a P. Musschenbroekem.
Polarizace dielektrika
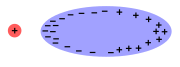
V izolantu nejsou nosiče elektrického náboje volné; vložením do elektrického pole jiného nabitého tělesa proto nedojde k jejich přeskupení na povrch. Nosiče elektrického náboje obou polarit jsou vázány v atomech, molekulách či krystalových buňkách izolantu. Jejich polohy se však mohou mikroskopicky posunout a původně neutrální atomy tak změnit na dipóly, nebo polární molekuly či polární krystalové buňky uspořádat - v obou případech budou dipóly většinově orientovány souhlasným nábojem od vnějšího nabitého tělesa a budou tak zeslabovat výsledné pole v izolantu. Tento jev se nazývá polarizací dielektrika.
Polarizaci dielektrika objevil Johann Carl Wilcke.
Polarizace dielektrika nemusí být vyvolána pouze elektrickým působením nabitého tělesa, ale může k ní dojít spontánně vzájemným spolupůsobením a jím vyvolaným samovolným uspořádáním polárních molekul nebo polárních krystalových buněk (tzv. ferroelektrický jev).
Elektrizace těles; statická elektřina
Pod elektrostatické jevy v širším slova smyslu se někdy zahrnují též jevy oddělení kladného od záporného náboje, hromadění náboje stejné polarity a přenosu elektrického náboje mezi tělesy (elektrizace) a projevy tzv. statické elektřiny, způsobené nashromážděním nábojů na povrchu různých těles a předmětů a jejich výměně při kontaktu s jinými povrchy. Alespoň jedno z těles je přitom nevodivé, tj. jeho povrch má vysoký elektrický odpor, což umožňuje shromáždění a setrvání nosičů náboje (u vodiče by se nosiče souhlasného náboje vzájemným odpuzováním rozptýlily. K zamezení negativních projevů statické elektřiny je proto potřeba zamezit vzniku nábojů (např. antistatické nástřiky povrchů) nebo zajistit stálý odvod náboje vodivým spojením, např. uzemněním.
Elektrický náboj „vzniká“ (resp. k oddělení nosičů kladného a záporného náboje dochází) např:
- kontaktem těles rozdílného materiálu; příčinou přitom může být např.:
- rozdílná výstupní práce elektronu - u dvou kovů)
- triboelektrický jev - u dielektrik (při jejich tření se rozloží po větším povrchu nevodiče, což umožní oddělení větších nábojů)
- elektrochemický proces (Voltův jev)
- zelektrováním vodiče elektrostatickou indukcí,
- teplem (tzv. pyroelektrický jev),
- tlakem (tzv. piezoelektrický jev),
- zářením (tzv. vnitřní fotoelektrický jev).
Náboj se předá z jednoho tělesa na druhé:
- dotykem
- sršením (zejména z hrotů těles) či výbojem (jedná se o vlastně o elektrický proud v plynech či vakuu, přesto bývá někdy diskutován v rámci elektrostatických jevů v širším slova smyslu)
- vedením (elektrickým proudem) – již mimo rámec elektrostatiky.
Na principech elektrizace třením, sršení náboje a rozdělení nábojů po povrchu vodiče pracuje Van de Graafův generátor.
Jako příklady negativních následků neutralizace nábojů statické elektřiny výbojem lze uvést spontánní explozi obilních sil či poškození elektronických součástek během jejich výroby. Vedle fyzických antistatických opatření, jako je chemické ošetření povrchů a uzemnění, lze uvést i „administrativní“ opatření proti negativním následkům – např. známý zákaz používání kanystrů z některých plastů pro vznětlivé látky (benzin).
Vymezení předmětu elektrostatiky
Elektrostatika je součástí teorie elektromagnetického pole.
Zabývá se jevy spojenými se statickým (tj. ustáleným, časově neproměnným) vzájemným silovým působením elektrických nábojů a jimi vytvořeným elektrostatickým polem:
- Definuje důležité charakteristiky elektrostatického pole a charakteristiky látkového prostředí důležité z hlediska elektrického silového působení.
- Poskytuje teoretické prostředky pro popis elektrostatického pole.
- Formuluje základní zákonitosti klidového elektrického působení částic a těles.
- Zabývá se metodami řešení elektrostatického pole pro zadané podmínky (tj. stanovení průběhů důležitých veličin).
- Stanoví obecné důsledky zákonitostí elektrostatického pole na energetické (termodynamické) zákonitosti systémů.
- Je teoretickým základem pro řešení statických problémů elektrotechniky.
Elektrostatika nestuduje pohyb nábojů ani účinky pohybujících se nábojů, a nezabývá se ani elektrickým polem (i kdyby bylo časově konstantní) vzniklým elektromagnetickou indukcí v proměnném magnetickém poli.
Důležité veličiny elektrostatiky
- Poznámka: Tento přehled uvádí pouze stručné charakteristiky a jednotky jednotlivých veličin a slouží spíše jako rozcestník ke speciálním stránkám.
- Elektrický náboj; doporučená značka[2]
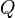 ; jednotka SI: coulomb, značka C
; jednotka SI: coulomb, značka C
popisuje zdroje elektrického silového působení - Intenzita elektrického pole; doporučená značka
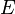 ; jednotka SI: volt na metr, značka V/m
; jednotka SI: volt na metr, značka V/m
popisuje vektorově silové účinky elektrického pole a na rozdíl od působící elektrické síly je nezávislá na náboji testovací částice - Elektrický potenciál; doporučené značky
 ,
,  ; jednotka SI: volt, značka V, resp.
; jednotka SI: volt, značka V, resp. - Elektrické napětí (rovné rozdílu elektrického potenciálu dvou míst); doporučená značka
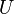 ; jednotka SI: volt, značka V
; jednotka SI: volt, značka V
popisují elektrostatické pole skalárně a charakterizují jeho schopnost konat elektrickou práci nezávisle na náboji testovací částice - Elektrická kapacita; doporučená značka
 ; jednotka SI: farad, značka F
; jednotka SI: farad, značka F
popisuje schopnost soustavy vodičů jímat elektrický náboj - Elektrická polarizace; doporučená značka
 ; jednotka SI: coulomb na čtverečný metr, značka C/m2
; jednotka SI: coulomb na čtverečný metr, značka C/m2
popisuje vektorově dodatečné elektrické pole vzniklé v dielektriku jeho polarizací - Elektrická indukce; doporučená značka
 ; jednotka SI: coulomb na čtverečný metr, značka C/m2
; jednotka SI: coulomb na čtverečný metr, značka C/m2
popisuje vektorově elektrické pole v libovolném prostředí jako výsledek působení pouze volných nábojů
Důležité zákony, vztahy a věty
Coulombův zákon
- Podrobnější informace naleznete v článku Coulombův zákon.
Základním zákonem elektrostatiky je Coulombův zákon. Podle něj je elektrická síla působící mezi dvěma bodovými náboji přímo úměrná součinu jejich nábojů a nepřímo úměrná druhé mocnině jejich vzdálenosti. Navíc platí tzv. princip superpozice, podle kterého vzájemné elektrické působení dvou nábojů není ovlivněno elektrickým působením dalších nábojů, tedy že elektrické síly lze vektorově sčítat.
Spojenou formulaci Coulombova zákona a principu superpozice lze zapsat vztahem pro sílu, kterou působí bodové náboje 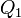 ,
, 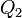 ,… v místech daných polohovými vektory
,… v místech daných polohovými vektory 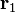 ,
, 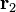 ,… na bodový náboj
,… na bodový náboj 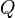 v místě daném polohovým vektorem
v místě daném polohovým vektorem 
 ;
; 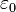 je univerzální konstanta, tzv. permitivita vakua.
je univerzální konstanta, tzv. permitivita vakua.
Gaussova věta
- Podrobnější informace naleznete v článku Gaussův zákon elektrostatiky.
Z Coulombova zákona a principu superpozice lze odvodit ekvivalentní Gaussovu větu, podle které: Tok vektoru intenzity elektrického pole uzavřenou plochou je roven celkovému náboji plochou uzavřenému, dělenému permitivitou vakua:
Gaussovu větu lze přepsat do tvaru pro elektrickou indukci a pouze volné náboje: Tok vektoru elektrického indukce uzavřenou plochou je roven celkovému volnému náboji (tj. bez vázaných polarizačních nábojů v dielektriku) plochou uzavřenému:
V oblasti, kdy lze považovat rozložení elektrického náboje za (makroskopicky) spojité, popsatelné objemovou hustotou elektrického náboje  , lze Gaussovu větu přepsat do diferenciálního tvaru:
, lze Gaussovu větu přepsat do diferenciálního tvaru:
resp. (tzv. třetí Maxwellova rovnice):
Rovnice plynoucí z nevírovosti elektrostatického pole
Z Coulombova zákona vyplývá, že elektrostatické pole je pole potenciálové, nevírové. To znamená, že celková elektrická práce vykonaná polem při pohybu náboje po uzavřené dráze je nulová, což lze zapsat vztahem:
 , resp. v diferenciálním tvaru:
, resp. v diferenciálním tvaru: 
- Pozn.: Nevírovost je také důvodem, proč se elektrostatika nezabývá elektrickým polem (i kdyby bylo časově konstantní) vzniklým elektromagnetickou indukcí v proměnném magnetickém poli. Toto pole je totiž vírové.
Intenzita elektrického pole lze proto vyjádřit pomocí potenciálu:
a dosazením do Gaussovy věty získáme Laplaceovu-Poissonovu rovnici:
Rovnice má stejný tvar pro volné náboje a tzv. měkké dielektrikum (u kterého je elektrická indukce přímo úměrná intenzitě elektrického pole), namísto permitivity vakua je pak nutno dosadit permitivitu prostředí. V oblastech bez (volných) nábojů je pravá strana rovnice nulová.
Věta o jednoznačnosti řešení
Hledání potenciálu soustavy vodičů vyhovujícího Laplaceově-Poissonově rovnici a zadaným okrajovým podmínkám představuje tzv. základní úlohu elektrostatiky.
V elektrostatice se dokazuje věta o jednoznačnosti řešení:
Jsou-li jako okrajové podmínky zadány:
- potenciály na povrchu vodičů, nebo náboje vodičů,
- limitní hodnota potenciálu v nekonečnu, nebo hodnota na obálce zkoumané oblasti,
pak má Laplaceova-Poissonova rovnice v oblasti mezi vodiči nejvýše jedno řešení, vyhovující těmto podmínkám.
Najdeme-li tedy jakoukoli speciální metodou řešení základní úlohy elektrostatiky, věta o jednoznačnosti je zárukou, že se jedná o správné hledané řešení – jiné řešení totiž neexistuje.
Věty pro rozhraní dvou prostředí
V elektrostatice se dokazují následující věty o elektrostatickém poli u rozhraní dvou prostředí:
- Elektrický potenciál v celém objemu vodiče je konstantní – jeho povrch je proto ekvipotenciální plocha. V každém vnitřním bodě vodiče je tedy výsledná intenzita elektrického pole (tj. od vnějších zdrojů a od indukovaných nábojů na povrchu) nulová.
- Coulombova věta: Tečná složka vektoru intenzity elektrostatického pole je na povrchu vodiče nulová (vektor intenzity je kolmý k povrchu vodiče). Normálová (tj. kolmá) složka vektoru intenzity elektrostatického pole v bezprostřední blízkosti povrchu vodiče je rovna podílu plošné hustoty elektrického náboje a permitivity vakua. (Pro lineární dielektrikum je elektrická indukce v bezprostřední blízkosti povrchu vodiče rovna plošné hustotě náboje.)
- Elektrický potenciál je všude spojitý (včetně povrchu vodičů a rozhraní dielektrik) s výjimkou nábojové dvojvrstvy (plošné rozložení bodových elektrických dipólů s orientací dipólového momentu kolmou k dané ploše).
- Na hranici dvou dielektrik je spojitá tečná složka vektoru intenzity elektrostatického pole a normálová složka vektoru elektrické indukce.
Věty o multipólovém rozvoji
Potenciál elektrostatického pole nábojů libovolně rozložených v omezené části prostoru lze (za předpokladu konstantního, zpravidla nulového, potenciálu v nekonečnu ve všech směrech) lze vhodně popsat jako superpozici potenciálů elektrických multipólů:
- Elektrostatické pole libovolné soustavy nábojů, kterou lze uzavřít do myšlené koule, je vně této koule totožné s polem soustavy bodových multipólů umístěných ve středu této koule. Moment multipólu nejnižšího řádu je přitom nezávislý na volbě středu této koule.
Speciálně platí:
- Potenciál libovolného rozložení náboje na úsečce lze vně koule úsečce opsané (tj. průměr koule je dán touto úsečkou) vyjádřit jako potenciál bodových axiálních multipólů umístěných ve středu této koule.
Energie elektrostatického pole
- Podrobnější informace naleznete v článcích Elektrická energie a Elektrická práce.
Energie dané soustavy nabitých vodičů lze vyjádřit pomocí potenciální energie jednotlivých nábojů v potenciálu pole. Na zvýšení náboje vodiče o 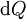 je potřeba vykonat elektrickou práci
je potřeba vykonat elektrickou práci 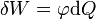 ; to představuje zároveň i změnu energie vzájemného působení nábojů a pole jimi vytvořeného.
; to představuje zároveň i změnu energie vzájemného působení nábojů a pole jimi vytvořeného.
V případě vzájemného působení nabitých vodičů (jakož i bodových nábojů) bude jejich (interakční) energie (pro zamezení záměny s intenzitou elektrického pole je v tomto článku značena  ):
):
 , kde
, kde 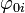 je potenciál vodiče (na povrchu i uvnitř konstantní).
je potenciál vodiče (na povrchu i uvnitř konstantní).
V případě spojitého rozložení náboje s hustotou  lze vztah pro energii přepsat jako integrál přes oblast rozložení náboje:
lze vztah pro energii přepsat jako integrál přes oblast rozložení náboje:
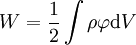 .
.
Energii lze také vyjádřit pomocí veličin elektrostatického pole (intenzity elektrického pole a elektrické indukce) a interpretovat ji jako energii vytvořeného pole mezi vodiči (resp. bodovými náboji). Elementární změna energie bude dána vztahem:
 .
.
Pro tzv. měkké dielektrikum (u kterého je elektrická indukce přímo úměrná intenzitě elektrického pole) lze pak celkovou energii vyjádřit jako:
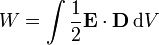 ,
,
a výraz 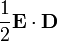 interpretovat jako hustotu energie elektrostatického pole.
interpretovat jako hustotu energie elektrostatického pole.
Věty o energii a silách v elektrostatickém poli
V elektrostatice se dokazují následující věty:
- Vložení nenabitého vodiče do elektrického pole pevné soustavy nábojů zmenší celkovou energii pole.
- Earnshawova věta: Nabité těleso nelze udržet v elektrostatickém poli ve stabilní rovnováze pouze elektrostatickými silami.
- Thomsonova věta: Náboje na soustavě pevných vodičů v dielektriku se samy rozloží po povrchu těchto vodičů tak, aby energie výsledného elektrostatického pole byla minimální.
Metody řešení elektrostatického pole
V teorii parciálních diferenciálních rovnic jsou zpracovány obecné metodiky řešení Laplaceovy-Poissonovy rovnice. Podobně numerická matematika dává návody pro výpočet řešení této rovnice při zadaných okrajových podmínkách.
V konkrétních případech řešených v elektrostatice a teoretické elektrotechnice lze však často využít jednodušší analytické metody, vycházející ze znalosti fyzikální podstaty problému a využívající symetrií a jiných vhodných okolností speciálních případů. Mezi takové metody patří:
- Výpočet přímo z Coulombova zákona a principu superpozice
Tento postup je možno vhodně použít pouze u soustav malého počtu bodových nábojů
- Použití Gaussovy věty
Tuto metodu lze vhodně použít u symetrických případů, kde se zjednoduší integrace. Takovými případy jsou např. pole soustav s kulovou, válcovou nebo rovinnou symetrií (pole kulového vodiče případně několika soustředných kulových vrstev vodičů a dielektrik, pole válcového vodiče případně několika souosých válcových vrstev, pole soustavy rovnoběžných deskových vodičů ve vzdálenosti podstatně menší než jsou rozměry desek) a superpozice polí malého počtu takových soustav. - Metoda nábojového zobrazení (zrcadlení a kulová resp. válcová inverze)
Tato metoda využívá větu o jednoznačnosti řešení a je vhodně použitelná pro soustavy vodivé plochy (nebo plošného rozhraní dielektrik) a bodového náboje (případně lineárního vodiče rovnoběžného s plochou). Způsob řešení spočívá v tom, že k původním nábojům se zavedou symetrické náboje s opačnou polaritou, a tím se dosáhne shody ekvipotenciálové plochy s danou plochou vodiče. Podle věty o jednoznačnosti to bude zároveň hledané řešení. Symetrickým zobrazením je pro rovinné plochy zrcadlení, pro válcové a kulové je to válcová resp. kulová inverze.
Takovými vhodnými případy jsou např.:- rovinná plocha a malý počet bodových nábojů
- rovinná plocha a malý počet s ní rovnoběžných lineárních vodičů
- kulová plocha a bodový náboj nebo dvě nesoustředné kulové plochy
- válcová plocha a bodový náboj nebo dvě nesoustředné válcové plochy
- plocha ve tvaru klínu s vrcholovým úhlem rovným celočíselné části 360° a malý počet bodových nábojů
- plocha ve tvaru klínu s vrcholovým úhlem rovným celočíselné části 360° a malý počet s ní rovnoběžných lineárních vodičů.
- Metoda komplexních potenciálů a konformních zobrazení
Tuto metodu lze vhodně použít pro řešení polí nezávislých na jednom směru (v průmětu v tomto směru se bude jednat o rovinné úlohy) kolem vodičů, jejichž tvar lze konformním zobrazením převést na rovinu (v průmětu na přímku). Potenciál se popíše analytickou funkcí komplexní proměnné, u které bude zaručeno splnění dvourozměrné Laplaceovy-Poissonovy rovnice, přičemž reálná část bude popisovat ekvipotenciálové křivky (průmět ekvipotenciálových ploch), imaginární část siločáry. Bude-li tato funkce konformně zobrazovat daný tvar plochy (v průmětu křivky) na rovinu (v průmětu na přímku), bude její reálná část určovat rovnice ekvipotenciál.